
Una delle motivazioni dietro la spinta all’introduzione della programmazione dei computer in giovane età (=coding) è quella per cui questa pratica insegna il pensiero computazionale, che è un modo di affrontare i problemi in maniera scientifica. Anche se Jeannette Wing si è affannata a dire che non si tratta di insegnare ai bambini a pensare come i computer, e Seymour Papert a predicare che bisogna insegnare ai computer come se fossero bambini, questo tema resta nell’aria. Computazionale significa “razionale, finito, corretto, misurabile” eccetera. In pratica, imparare il pensiero computazionale significa, per ogni problema, saper immaginare un algoritmo che lo risolva. Questo algoritmo deve essere eseguibile praticamente da un computer: non deve contenere errori, non deve basarsi su termini ambigui, non deve richiedere un tempo infinito o una memoria infinita per arrivare alla soluzione.
Però gli algoritmi si pensano (e poi si scrivono) diversamente a seconda del linguaggio, e a seconda del tipo di linguaggio che si ha in mente. Usare un linguaggio semplice quando si è ai primi passi è sicuramente una buona idea; ma cosa significa “semplice”? Può significare che costringe ad usare dei concetti e delle operazioni di base, vicine a quelle che sa fare il computer; oppure che spinge a nascondere i dettagli e a concentrarsi “semplicemente” sulla struttura dei dati e sugli obiettivi.
Insegnare ai bambini una forma di pensiero computazionale che li abitua a pensare nei termini del primo significato di “semplicità” rischia di creare più problemi – in futuro – di quelli che risolva adesso.
Voglio provare a spiegare questa differenza con un piccolo esempio.
Partiamo da Snap!, un ambiente di programmazione che pochi conoscono, che assomiglia molto a Scratch (ne è derivato) ma ha delle differenze importanti. Intanto è nato all’Università di Berkeley, dall’altra parte degli USA rispetto a Stanford, dove è nato Scratch. Poi ha un target più ampio, nel senso che può essere usato da bambini ma anche da ragazzi più grandi, perché è basato su un modello di linguaggio più potente di quello che sta sotto Scratch. Le differenze tra Snap! e Scratch sono poco visibili ad un primo approccio (si possono disegnare girandole o creare scenette animate con entrambi), ma sono molto profonde. Ne elenco solo tre fondamentali:
- A differenza di Scratch, in Snap! si possono creare funzioni, cioè procedure che alla fine restituiscono un valore, e questo è molto comodo perché permette di costruire delle catene di funzioni che si applicano ai risultati di altre funzioni.
- In secondo luogo, in Snap! ci sono delle funzioni per creare e gestire vere liste (di numeri, di lettere, di parole, ma anche di sprite, o di qualsiasi oggetto).
- Inoltre le funzioni possono essere usate come oggetti da altre funzioni. In altre parole: una funzione si può applicare non solo a oggetti semplici (come numeri, lettere) ma anche ad altre funzioni. In aritmetica conosciamo questo tipo di cose: la moltiplicazione è l’applicazione ripetuta della funzione somma.
Il terzo punto è particolarmente utile quando si vogliono trattare delle serie di dati. Se vogliamo trasformare una lista di numeri, o di lettere, o di parole, in qualche altra cosa dobbiamo applicare una trasformazione ad ognuno degli elementi della lista per ottenere una nuova lista; avere un linguaggio che permetta di fare direttamente questo tipo di operazioni permette di concentrarsi sul problema, e non sul meccanismo delle soluzione.
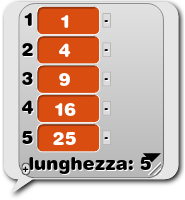
Mettiamo, per esempio, di voler generare la lista dei quadrati dei primi 10 numeri interi. Partendo da una lista di numeri interi, vogliamo moltiplicare ogni numero per se stesso. Cioè da 1,2,3,4,5… vogliamo ottenere 1,4,9,16,25 …
Questo in Scratch si può fare così:
- crea una lista di numeri interi e dagli il nome “numeri”
- crea una seconda lista e dagli un nome “quadrati”
- crea un contatore e dagli il nome “i”, e valore 0
- ripeti tante volte quanto è la lunghezza della lista “numeri”:
- aumenta “i” di 1
- moltiplica l’elemento i della lista “numeri” per se stesso
- aggiungi il risultato alla lista “quadrati”
Saltando la parte di creazione delle variabili, ecco i blocchetti:
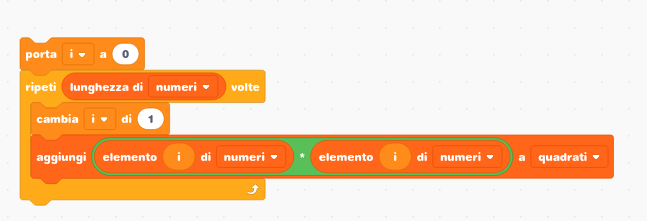
E’ semplice, sì, ma è anche un modo di pensare molto meccanico, che segue esattamente quello che succede “sotto il cofano”. Siamo noi che ci adeguiamo al modo di lavorare del computer, e non viceversa. Arrivare a questa formulazione non è banale: bisogna imparare a pensare in un certo modo. Bisogna imparare il concetto di contatore, di indice di una lista, quello di ciclo, di test di terminazione, eccetera. Sono gli elementi di base della programmazione classica.
Proprio questo è uno dei limiti dell’approccio “computazionale” di cui parlavamo sopra: si impara a pensare come un computer, o meglio secondo gli schemi che il linguaggio di programmazione che usiamo (in questo caso Scratch) mette a disposizione.
Da un lato questo apprendimento ha degli aspetti positivi: ogni volta che ci poniamo un limite impariamo nuovi modi di risolvere problemi. Dall’altro, restare dentro quei limiti non ci permette di andare molto lontano. Potrebbe esserci (non è mai stato studiato a fondo) una forma di imprinting per cui il primo modello di programmazione imparato resta quello fondamentale, un po’ come la lingua madre. Se i bambini imparano a usare i cicli per scorrere le liste, poi continueranno a farsi venire in mente questa modalità anche in futuro.
Ma usare i cicli è solo uno dei possibili modi di risolvere il problema dei quadrati. Ce ne sono altri, che dipendono dal linguaggio che si usa.
In Snap! si possono disporre i blocchetti esattamente nello stesso modo che in Scratch:

Ma si può fare anche qualcosa di diverso, più semplice e soprattutto più vicino alla struttura del problema.
Per risolvere il problema dei quadrati dei numeri interi non siamo costretti a pensare in termini di contatori e di indici, non dobbiamo per forza preoccuparci di sapere quando fermare il processo, dove mettere i risultati. Queste sono cose che riguardano la meccanica dell’algoritmo, non il problema in sé.
Qual era la cosa che volevamo fare, l’idea iniziale? Applicare la funzione “moltiplica per se stesso” a tutti gli elementi di una lista. Bene, allora cominciamo dalla lista

Questo blocchetto è una funzione che restituisce una lista costruita con gli oggetti che mettiamo negli spazi bianchi, in questo caso i primi cinque numeri interi. Non abbiamo bisogno di creare una variabile perché la funzione restituisce sempre quello che ci serve. Ora possiamo disporre i blocchetti in modo da rispettare esattamente l’idea originale di applicare la moltiplicazione alla lista:

Finito. Non c’è altro da fare. Questo blocchetto (“applica”) fa da solo tutto il lavoro: prende il primo elemento della lista, lo inserisce nei due buchi del blocchetto verde, esegue la moltiplicazione e mette da parte il risultato, poi passa al successivo. Alla fine restituisce una nuova lista con i risultati.
La presenza del blocchetto “applica” è una delle caratteristiche di Snap! (e dei linguaggi funzionali a cui si ispira) a cui facevamo riferimento prima. E’ una funzione che lavora su altre funzioni. Usando questo approccio, non ci servono variabili, contatori, cicli. Per certi versi, è molto più intuitivo e vicino al problema questo approccio di quello precedente, in cui dovevamo introdurre una serie di concetti di supporto.
In Snap! c’è un’altra maniera di ottenere questo risultato, ancora più semplice di quella che abbiamo visto adesso. Torniamo all’idea di partenza: “moltiplicare ogni numero di una lista per se stesso”. Ma invece di moltiplicare ogni numero per se stesso, possiamo partire da due liste identiche, e moltiplicare ogni elemento della prima lista per il corrispondente elemento della seconda.
Proviamo a fare esattamente questo:

Il risultato è lo stesso. In sostanza, l’operazione “moltiplicazione” normalmente si applica a dei numeri; ma in Snap! è stata estesa per applicarsi anche a delle liste. Naturalmente potremmo pensare di utilizzarla anche per moltiplicare due liste diverse, o per moltiplicare una lista per un numero singolo. Forse funziona anche con altre operazioni? Proviamo con l’operazione “elevamento a potenza”:

Funziona. Ed è abbastanza chiaro che è molto più semplice di tutto l’ambaradam che avevamo dovuto mettere in campo prima. Questa modalità ci libera di tutta la parte meccanica e ci spinge invece verso una maniera diversa di concepire il problema che volevamo risolvere, che a sua volta ci apre la strada verso altre possibilità.
In conclusione: attenzione al linguaggio che si sceglie, e non confondiamo la razionalità con la meccanicità.
Lascia un commento
Devi essere connesso per inviare un commento.